secrets of successful stone skipping —
A combination of gyro effect and Magnus effect influences the deflection of trajectory
Jennifer Ouellette
–

Enlarge / Experiments by Chinese physicists have shed further light on the intricate physics involving in skipping a stone across the water’s surface. Their findings revealed key factors that could influence spaceflight water landings after re-entry.
Learning how to skip stones across a lake or pond is a time-honored childhood tradition. The underlying physics of skipping stones could also be a useful model for landing aircraft or spacecraft on water, according to a recent paper published in the journal Physics of Fluids. Chinese physicists have built just such a model, and they used it to further clarify the key determining factors behind how many times a stone (or spacecraft) will bounce upon hitting the water.
Skipping stones is just the sort of natural everyday phenomenon that would fascinate physicists, even though at first glance the basic concepts seem simple. It all comes down to spin, speed, shape of the stone, and angle. As the stone hits the water, the force of impact pushes some of the water down, so the stone, in turn, is forced upwards. If the stone is traveling fast enough to meet a minimum velocity threshold, the stone will bounce; if not, it will sink. A round, flat stone is best, simply because its surface area displaces more water as it skips.
Experiments in 2004 by French physicists Lyderic Bocquet and Christophe Clanet demonstrated as much. They built a catapult device to toss aluminum disks at a tank of water and then recorded the splashes with high-speed video. They learned that the bouncing stone must be spinning at a minimal rate of rotation (at least once during its collision time) in order to be stable. In other words, a skipping stone relies on the gyroscopic effect, in which a body rotating around its own axis tends to maintain its own direction. (It’s also what stops a spinning top from tipping over.) Experienced stone-skippers typically apply this rotation to the stone with a simple flick of the finger.
Bocquet and Clanet’s experiments helped them determine how best to maximize the number of bounces. The obvious solution is to throw the stone as fast as possible, since the number of bounces is proportional to the throwing speed. But this must be balanced against being able to control the velocity and direction of the throw. Even with their catapult machine, the French physicists could only achieve about 20 bounces—significantly less than the current world record of 88 skips, set in 2013.
They gleaned further insight by examining what makes the stone stop skipping. It’s not because the stone slows down; rather, its trajectory flattens over time. Bocquet and Clanet concluded that this occurs because of the angle at which the stone moves, relative to the water’s surface. The stone displaces more water when it moves downward than when it’s moving upward, so over time less and less transfer of momentum occurs, gradually reducing the lift. Eventually the stone no longer has sufficient energy to skip, and it will sink. Their experiments showed that the optimal angle between the plane of the stone and the water’s surface is between 10 and 20 degrees.
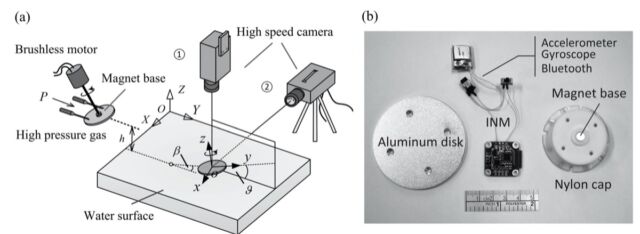
Enlarge / Schematic diagram of launching device and close-up of data acquisition system.
Kun Zhao
In 2014, a Utah State University team experimented with bouncing elastic spheres across the surface of water, capturing the dynamics with a high-speed camera. The spheres are more elastic than rocks and thus deform into disks as they hit the water, taking on the ideal shape for a skipping stone. Because the plastic spheres can deform independent of the angle at which they hit the water and have a lower velocity threshold, achieving more bounces with them is much easier. In fact, anyone can achieve a good 20 skips with a plastic sphere after a mere 10 minutes of practice, according to USU physicist and co-author Tadd Truscott.
Beyond the fun factor, there’s a long history of scientists applying the lessons of skipping stones to real-world applications. Around 1578, for instance, mathematician William Bourne noted that cannonballs fired from ships at a sufficiently low angle could ricochet across the water’s surface, bouncing onto decks and breaking masts on the the target ships. And during World War II, British engineer Barnes Wallis came up with a “bouncing bomb” design, in which the weapon bounced across the water before striking the target, then sank and exploded underwater, akin to a depth charge. The Royal Air Force used bouncing bombs against Germany in 1943.
More directly relevant to the current paper, in 1929, Theodore von Karman conducted several experiments to determine the maximum pressure on seaplanes during water landings, and in 1932, Herbert Wagner showed that the takeoff and landing of a seaplane was essentially all about impacts and sliding on a liquid surface. “[Wagner] pointed out that the impact processes are predetermined uniquely by the initial motion of the liquid and the course of the movement of the body,” the Chinese co-authors of this latest paper wrote in their introduction.
For their new research, the Chinese team focused on bouncing (skipping) and surfing, in which the disk or stone skims the surface and never bounces. The researchers came up with their own theoretical model of the phenomenon that incorporated not only the aforementioned gyroscopic effect, but also the Magnus effect. It’s long been known that the movement of a baseball, for instance, creates a whirlpool of air around it. The raised seams churn the air around the ball, creating high-pressure zones in various locations (depending on the type of pitch) that can cause deviations in its trajectory. Something similar occurs with skipping stones.
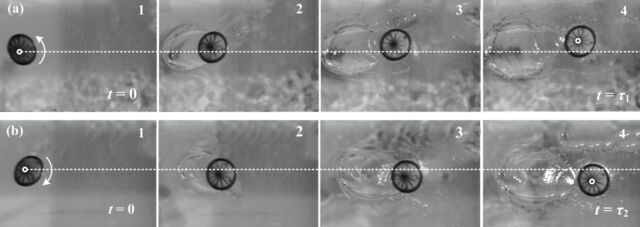
Enlarge / Chronophotography of the skipping stone, obtained with an aluminum disk.
Jie Tang et al./Physics of Fluids 2021
To test their model, the Chinese scientists created an experimental setup involving a flat aluminum disk and a launching system with a brushless motor to ensure the disk could reach the necessary speeds. The launching system used puffs of air from a compressor to control the disk’s speed as it traveled toward the water. The researchers attached a nylon cap to the disk, connecting it to the launcher via a magnetic base. The cap also held an inertial navigation module to measure and collect the data during launch, “flight,” and landing, transmitting that data to a computer via a Bluetooth connection.
The team found that the critical threshold for vertical acceleration is four times the acceleration due to gravity (4 g). The disk or stone will more likely surf if the vertical acceleration is a bit smaller (3.8 g), while the minimum threshold at which a stone has the potential to skip is 3.05 g.
The researchers also determined that it’s the combination of the gyro effect and the Magnus effect—both produced as the spinning stone hits the fluid—that influences the deflection of its trajectory. The direction of that deflection, in turn, is controlled by the stone’s direction of rotation (clockwise or counterclockwise). If the stone is rotating clockwise, the deflection bends to the right; if counterclockwise, the deflection bends to the left. The spinning helps stabilize the attack angle, thereby creating favorable conditions for the continuous bounce of the stone.
Thus, “Appropriate attack angles and horizontal velocities are the key factors in generating sufficient hydrodynamic forces to satisfy the conditions of bounce,” the authors concluded. “Our results provide a new perspective to advance future studies in aerospace and marine engineering,” added co-author Kung Zhao of the Beijing Electromechanical Engineering Institute. That perspective is most notable with regard to water landings of space flight re-entry vehicles and aircraft, as well as “hull slamming” (driving a ship’s hull into the cross section of the hull of another vessel), and improving torpedo designs.
DOI: Physics of Fluids, 2021. 10.1063/5.0040158 (About DOIs).

